DieselShip's Online Content Library

Q1) At a draught of 1.2 m in sea water of density 1025 kg/m³ the displacement of a ship is 1100 tonne and the height of the centre of buoyancy above the keel (KB) is 0.72 m.

Values of tonne per centimetre immersion (TPC) in sea water, for a range of draughts, are given in Table Q1.

(a) Calculate EACH of the following for a draught of 7.2 m in sea water:

(i)The displacement; (4)

(ii) The height of the centre of buoyancy above the keel (KB). (6)

(b) At a draught of 7.2 m, the height of the longitudinal metacentre above the keel (KML) is 135 m and the second moment of area of the waterplane about a transverse axis through midships is 1289670 m⁴. The centre of floatation is aft of midships.

Calculate the distance of the centre of floatation (LCF) from midships. (6)

Q2) A ship of 5000 tonne displacement floats at a mean draught of 7 m when in sea water of density 1025 kg/m³, but is unstable and has an angle of loll.

Hydrostatic particulars for the ship in the upright condition at the above displacement are as follows:

Centre of buoyancy above the keel (KB) = 3.706 m

Height of transverse metacentre above the keel (KM)= 5.926 m

tonne per centimetre immersion (TPC) = 10.0

To achieve a satisfactory stable condition with a metacentric height of 400 mm, a load of 500 tonne is added to the ship on the centreline at a Kg of 2.5 m.

Calculate EACH of the following, for the original unstable condition:

(a) The height of the original centre of gravity above the keel(KG); (12)

(b) The angle of loll. (4)

Note: The vessel may be considered ‘ wall-sided’ between the limits of draught,

hence: GZ=sin⁡θ (GM+1/2 BM tan² θ)

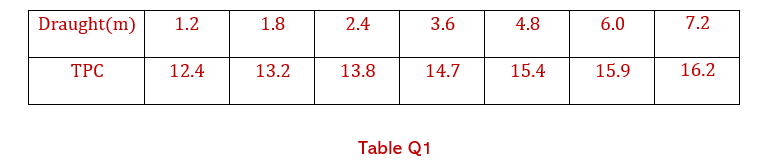
Q3. A Ship Of length 130 m has a light displacement Of 4800 tonne with the longitudinal centre of gravity 0.5 m aft of midships. Loading now takes place as given in Table Q3.

Using Worksheet Q3, extract the relevant data from the hydrostatic curves and hence determine the final end draughts of the vessel in sea water of density 1025 kg/ m³. (16)

Q4. A box shaped Vessel is 80 m long, 12 m wide and floats at a draught of 4 m.  A full width midship Compartment 15m tong is bilged. This results in the draught increasing to 4.75 m.

Calculate EACH of the following, using the lost buoyancy method:

(a) the permeability of the compartment; (4)

(b) the Change in metacentric height due to bilging the compartments. (12)

Q8) The following data applies to a ship operating on a particular voyage with a propeller of 6 m diameter having a pitch ratio of 0.9.

Propeller speed = 1.85 revs/s
Real slip = 33%
Apparent slip = 6%
Shaft power = 11000kW
Specific fuel consumption = 0.205 kg/kWhr

Calculate EACH of the following:

(a) the ship speed in knots; (3)

(b) the taylor wake fraction; (3)

(c) the reduced speed at which the ship should travel in order to reduce the voyage consumption by 30%; (2)

(d) the voyage distance if the voyage takes 30 hours longer at the reduced speed; (4)

(e) the amount of fuel required for the voyage at the reduced speed. (4)

Q11. Fig Q6 shows the results of progressive speed trials on a ship at a load displacement of 22350 tonne in sea water of density 1025 kg/m³ with a wetted surface area of 4860 m.

Using the data given below, calculate the shaft power required to achieve a service speed of 17 knots with a geometrically similar ship having a load displacement of 29245 tonne in sea water.

Propulsive coefficient based upon shaft power for both trial and service conditions = 0.68

Allowance for appendages and weather in trial condition = 8%

Allowance for appendages and weather in service condition = 20%

Note: Frictional coefficient for the 22350 tonne ship in sea water is 1.410

Frictional coefficient for the 29245 tonne ship in sea water is 1.406

Speed is in m/s with index (n) = 1.825