DieselShip's Online Content Library

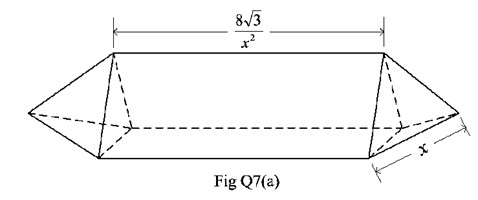
Q7. (a) A stainless steel tank is to be fabricated in the shape of a triangular prism with a regular tetrahedron at each end, as shown in Fig Q7(a).

The length of each edge of the tetrahedron is x metres.

The external surface area, A, of the tank is given by:

A = (3√3)/2 (x²+16/x)

Determine EACH of the following for the tank:

(i) dA/dx; (3)

(ii) the value of x which minimises the external surface area; (5)

Verify that the result obtained gives minimum surface area.

(iii) the minimum external surface area. (2)

(b) When a flywheel rotates through an angle of ϴ radians in t seconds, its angular velocity is given by dϴ/dt rads/s, and its angular acceleration is given by (d² ϴ)/(dt² ) rads/s².

For a certain flywheel ϴ = 27t – 3t² .

Determine EACH of the following for this flywheel:

(i) the angular velocity when t = 4; (3)

(ii) the angular acceleration; (1)

(iii) the time that elapses before the angular velocity is zero. (2)